Learning Lorenz with Neural ODE & Jacobian Matrix
Can a Neural ODE learn a chaotic system?
Motivation
.gif)
Lorenz-63
Lorenz-63 is a dynamical system that is non-linear and discrete-time. It is also both a chaotic and ergodic system.
Learning a Lorenz-63 from data would mean that statistics are reproduced: for example, auto-correlation is approaching to 0, lypunov spectrum is matching, and time average difference is converging.
This project is supervised by Dr. Nisha Chandramoorthy from Georgia Institute of Technology.
Through this project, questions we want to address include:
- 1. Can a Neural ODE learn a chaotic system?
- 2. If not, how can we make Neural ODE learn a chaotic system?
Method

This supervised learning problem aims solve the above empirical risk minimization problem. Experiment details are in the presentation file attached below.
New Training Algorithm:
We add new regularization term that accounts for the difference of Jacobian matrix.
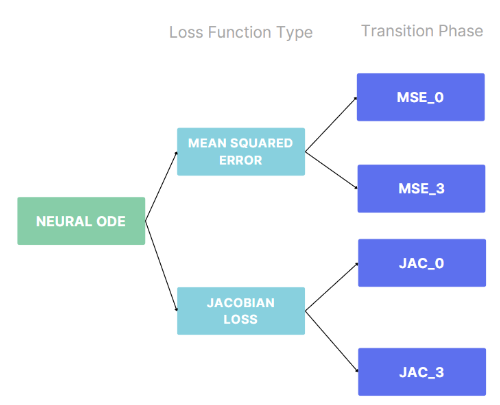
Summary of Two Experiment
Types of Model Created:
After two phase of experiment, we create 4 different models based on the loss function and training dataset
Findings

Original Neural ODE Simulation Learning Incorrect Dynamic
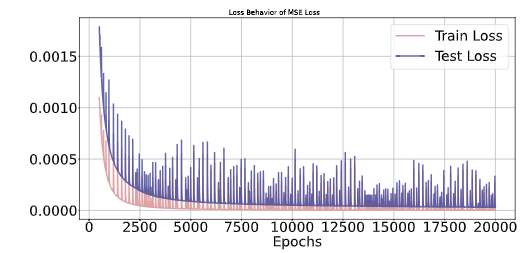
Train and Test Loss of Neural ODE
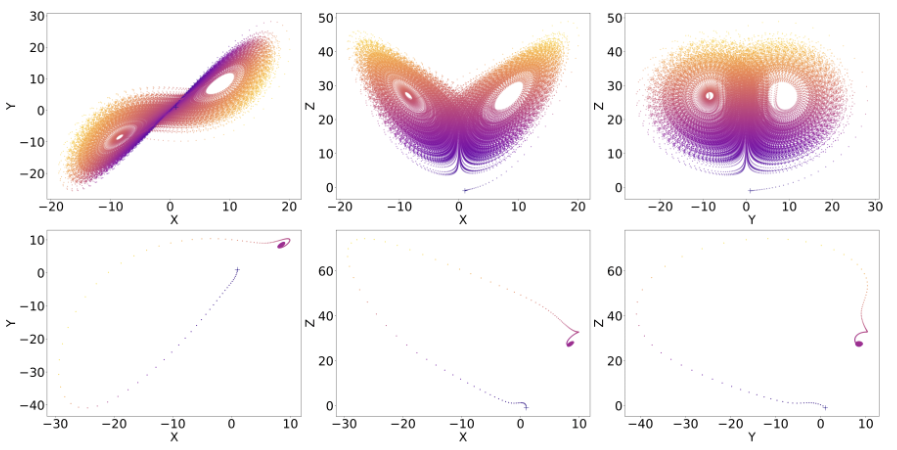
Phase Plot of True Lorenz and Neural ODE's Lorenz Orbit Starting From Outside of Attractor
Findings from the first phase of experiment:
- 1. As expected, training and test loss was small enough. And we would expect that generalization error will be low as well.
- 2. When tested with the initial point outside the attractor, solution generated by neural ODE showed different dynamics(some trajectories showed periodic or fixed point behavior).
- 3. Also, Neural ODE's Lyapunov Exponent did not match with the True Lyapunov Exponent.

New Neural ODE's Simulation
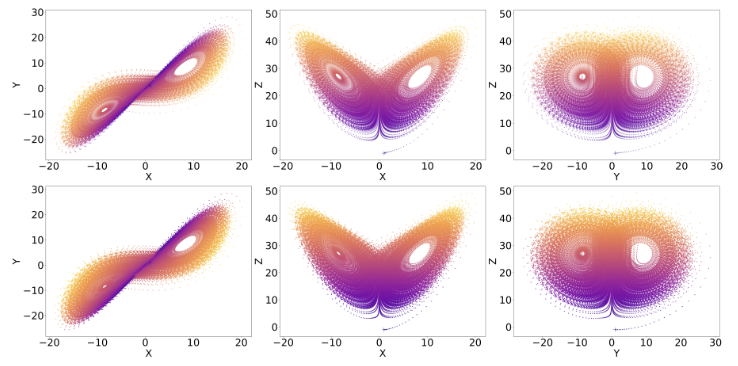
Phase Plot of True Lorenz and new Neural ODE's Lorenz Orbit Starting From Outside of Attractor
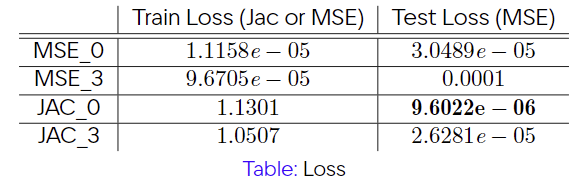
Train and Test Loss of Entire Models
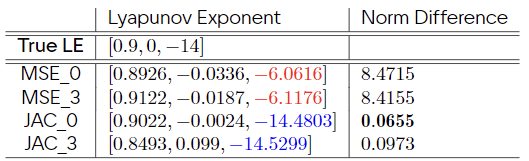
Table of Learned Lyapunov Spectrum
Findings from the second phase of experiment:
- 1. Along with the lowest test loss, Nerual ODE with Jacobian Loss showed the correct type of phase plot
- 2. While original Neural ODE did not learn the true Lyapunov Spectrum, the new Neural ODE learned the correct Lyapunov Spectrum, when taking account the numerical error of approximating Lyapunov Spectrum (QR method).
- 3. Adding Jacobian to the loss for Neural ODE learns the correct dynamics for lorenz-63 and its statistics, learning correct ergodic and chaotic system.
More experiment results can be found from the slides attached below.
Future Work
Want to explore if it works for other dynamical systems as well and understand why. Also, we must redefine generalization error to reflect true learning of ergodic dynamics.
More Information
For more detailed information, please look at the followings:
Presentation