N-CATS: Neural Chaotic Auto-Correlation for Time Series

Inspired by a recent discovery that the cryptocurrency market is a chaotic system, to learn dynamics from data with high volatility and noise, let's use chaos theory in training the model.

Due to high volatility, predicting cryptocurrency price is a challenging problem. But recent discoveries claim that the cryptocurrency market shows chaotic behavior. Thus, let's use that as prior knowledge and feed it to neural network!

Through this project, questions I want to address include:

• 1. Can we verify if the cryptocurrency market is indeed chaotic?
• 2. How do baseline models perform in predicting price?
• 3. How can we make a model learn market dynamics information?
• 4. How does the new model perform?

Dataset

Data:

• 1. Kaggle Bitcoin Historical Dataset.
• 2. The Dataset includes every 1 minute historical price in 2021.
• 3. Only used closing price, as a problem of interest is a univariate time series prediction.

Baseline:

• 1. LSTM
• 2. Neural ODE (Neural Ordinary Differential Equations)

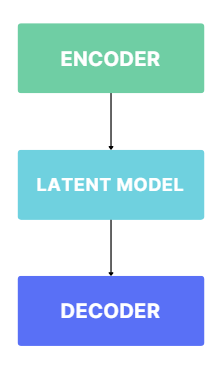
Architecture of N-CATS

New Model, N-CATS:

For the latent model, we can use any type of neural network, but for this project, let's use Neural Stochastic Differential Equation, from torchSDE.

Multi-step prediction of Neural ODE

Multi-step prediction of N-CATS

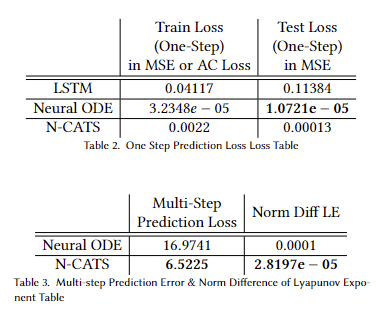
Table of Loss

Some of the findings includes:

• 1. When computing lyapunov exponent from the time-series dataset, I was able to verify that crypto-currency market is indeed chaotic as claimed by previous works. When using function from nolds package, lyap_r, layp_e, both returned a positive value (0.012, Maximum value of 0.2).
• 2. Found out that LSTM does not perform well in both short term and long term prediction with limited data. Neural ODE performs well in short term prediction but performs poorly in long term prediction.
• 3. Devised a new training algorithm for N-CATS. Instead of using Mean Squared Loss, I modified the loss function to match auto-correlation behavior of true time series as well.
• 4. N-CATS outperform industry standards(LSTM) and baseline(Neural ODE) by performing great in both short term and long term prediction. Also, when computing the norm difference of the Lyapunov Exponent, N-CATS showed the smallest error. Thus, among the all three, N-CATS is the best performing one.

Loss of N-CATS

Empirically speaking, auto-correlation loss seemed to be helpful in learning the dynamics only up to a certain point. It would be interesting to see if there is a way to learn more representative dynamics of the whole data rather than that of training data.

Novelty: When conducting this project, this was the first work to solve crypto-currency price prediction problem using auto-correlation in training deep learning model

For more detailed information, please look at the followings: Report

Presentation

Link to Github